Publications (en anglais)
-
Articles scientifiques
-
Livres et ouvrages collectifs
-
Mémoires
Voir aussi les profiles sur
Publons,
Orcid ou
Google Scholar.
1. Articles scientifiques
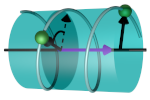
 | Protein-membrane interactions with a twist
Jordan Klein, Loréne Schad, Thérèse E. Malliavin, Martin Michael Müller |
Résumé
Soft Matter, 21: 4336, 2025.
 | Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic
Description of the Coiled-Coil Helix Bundle
Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller |
Résumé
Int. J. Mol. Sci., 25: 2481, 2024.
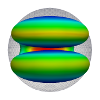 | Flexoelectric fluid membrane vesicles in spherical confinement
Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller |
Résumé
Plus d'infos
EPL, 131(1): 18001, 2020. Cf. aussi arXiv:2006.04475.
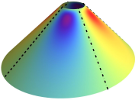 | Isometric bending requires local constraints on free edges
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
While the shape equations describing the equilibrium of an unstretchable thin sheet that is free
to bend are known, the boundary conditions that supplement these equations on free edges have remained elusive.
Intuitively, unstretchability is captured by a constraint on the metric within the bulk. Naïvely one would then
guess that this constraint is enough to ensure that the deformations determining the boundary conditions on these
edges respect the isometry constraint. If matters were this simple, unfortunately, it would imply unbalanced torques
(as well as forces) along the edge unless manifestly unphysical constraints are met by the boundary geometry. In this
article, we identify the source of the problem: not only the local arc-length but also the geodesic curvature need to
be constrained explicitly on all free edges. We derive the boundary conditions which follow. In contrast to conventional
wisdom, there is no need to introduce boundary layers. This framework is applied to isolated conical defects, both
with deficit as well, but more briefly, as surplus angles. Using these boundary conditions, we show that the lateral
tension within a circular cone of fixed radius is equal but opposite to the radial compression, and independent of
the deficit angle itself. We proceed to examine the effect of an oblique outer edge on this cone perturbatively
demonstrating that both the correction to the geometry as well as the stress distribution in the cone kicks in at
second order in the eccentricity of the edge.
 Fermer
Plus d'infos Fermer
Plus d'infos
Math. Mech. Solids, 24: 4051, 2019. Cf. aussi arXiv:1904.05855.
 | Helical Superstructure of Intermediate Filaments
Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić |
Résumé
Plus d'infos
Phys. Rev. Lett., 122: 098101, 2019. Cf. aussi arXiv:1803.04691.
 | Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows
Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller |
We present a numerical study of the time-dependent motion of a membrane vesicle in a
channel under an imposed flow. In a Poiseuille flow the shape of the vesicle depends on the flow strength,
the mechanical properties of the membrane, and the width of the channel. In a wide parameter region, the
emerging snaking shape shows an oscillatory motion like a swimmer flagella even though the flow is
stationary. We quantify this behavior by the amplitude and frequency of the oscillations of the vesicle's
center of mass. The influence of an amplitude modulation of the imposed flow on the dynamics and shape of
the snaking vesicle is also investigated. We find that this modulation---when sufficiently small---induces
a modulation in amplitude and frequency of the center of mass of the snaking vesicle. For large
modulation amplitudes transitions to static shapes are observed.
 Fermer Fermer
Phys. Rev. E, 98: 043111, 2018. Cf. aussi arXiv:1810.04500.
 | Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
We discuss how the equilibrium shapes of a confined toroidal fluid membrane vesicle
change when an adhesion between membrane and confining sphere is taken into account. The case without adhesion
was studied in Ref. [1]. Different types of solution were found and assembled in a phase diagram as a function of area
and reduced volume of the membrane. Depending on the degree of confinement the vesicle is either free, in contact along
a circle (contact-circle solutions) or on a surface (contact-area solutions). All solutions without adhesion are up-down symmetric.
When the container is adhesive, the phase diagram is altered and new kinds of solution without up-down symmetry are found.
For increasing values of adhesion the region of contact-circle solutions shrinks until it vanishes completely from the phase diagram.
 Fermer
Plus d'infos Fermer
Plus d'infos
IOP Conf. Series: MSE, 186: 012021, 2017.
 | Squeezed helical elastica
Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach |
Résumé
Plus d'infos
Eur. Phys. J. E, 39: 114, 2016. Cf. aussi arXiv:1606.03611.
 | How bio-filaments twist membranes
Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller |
Résumé
Soft Matter, 12: 5747, 2016.
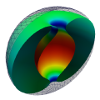 | Toroidal membrane vesicles in spherical confinement
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Résumé
Plus d'infos
Phys. Rev. E, 92: 032721, 2015. Cf. aussi arXiv:1509.00765.
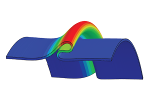 | Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate
Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
Int. J. Non-Linear Mech., 75: 115, 2015. Cf. aussi arXiv:1503.05030.
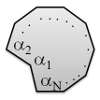 | Crunching Biofilament Rings
Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić |
We discuss a curious example for the collective mechanical behavior of coupled non-linear monomer units entrapped in a circular filament. Within a simple model we elucidate how multistability of monomer units and exponentially large degeneracy of the filament's ground state emerge as a collective feature of the closed filament. Surprisingly, increasing the monomer frustration, i.e., the bending prestrain within the circular filament, leads to a conformational softening of the system. The phenomenon, that we term polymorphic crunching, is discussed and applied to a possible scenario for membrane tube deformation by switchable dynamin or FtsZ filaments. We find an important role of cooperative inter-unit interaction for efficient ring induced membrane fission.
 Fermer
Plus d'infos Fermer
Plus d'infos
Europhys. Lett., 107(6): 68002, 2014. Cf. aussi arXiv:1408.6787.
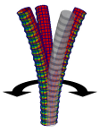 | Confotronic dynamics of tubular filaments
Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić |
Résumé
Plus d'infos
Soft Matter, 10(16): pp. 2836-2847, 2014. Cf. aussi arXiv:1312.3106.
 | Whirling skirts and rotating cones
Jemal Guven, J. A. Hanna, Martin Michael Müller |
Résumé
New J. Phys., 15: 113055, 2013. Cf. aussi arXiv:1306.2619.
 | Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo
Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte |
Résumé
J. Cell Sci., 126(8): 1806, 2013.
 | Dipoles in thin sheets
Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller |
Résumé
Plus d'infos
Eur. Phys. J. E, 36: 106, 2013. Cf. aussi arXiv:1212.3262.
 | Fluid membrane vesicles in confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
New J. Phys., 14: 095021, 2012.
 | Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity
Martine Ben Amar, Martin Michael Müller, Miguel Trejo |
The growth of a thin elastic sheet imposes constraints on its geometry such as its Gaussian curvature KG.
In this paper, we construct the shapes of sympetalous bell-shaped flowers with a constant Gaussian curvature. Minimizing the bending energies
of both the petal and the veins, we are able to predict quantitatively the global shape of these flowers. We discuss two toy problems
where the Gaussian curvature is either negative or positive. In the former case the axisymmetric pseudosphere turns out to mimic the correct
shape before edge curling; in the latter case, singularities of the mathematical surface coincide with strong veins. Using a variational
minimization of the elastic energy, we find that the optimal number for the veins is either four, five or six, a number which is deceptively
close to the statistics on real flowers in nature.
 Fermer
Plus d'infos Fermer
Plus d'infos
New J. Phys., 14: 085014, 2012. Choisi pour les Highlights of 2012.
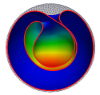 | Morphogenesis of membrane invaginations in spherical confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
Europhys. Lett., 97(6): 68008, 2012. Cf. aussi arXiv:1201.2518.
 | Conical instabilities on paper
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Résumé
Plus d'infos
J. Phys. A: Math. Theor., 45(1): 015203, 2012. Cf. aussi arXiv:1107.5008.
 | Interface-mediated interactions: Entropic forces of curved membranes
Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller |
Particles embedded in a fluctuating interface experience forces and torques
mediated by the deformations and by the thermal fluctuations of the medium.
Considering a system of two cylinders bound to a fluid membrane we show that
the entropic contribution enhances the curvature-mediated repulsion between
the two cylinders. This is contrary to the usual attractive Casimir force in
the absence of curvature-mediated interactions. For a large distance between
the cylinders, we retrieve the renormalization of the surface tension of a
flat membrane due to thermal fluctuations.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. E, 83(5): 051921, 2011. Cf. aussi arXiv:1011.1221.
 | Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann |
Résumé
Plus d'infos
Phys. Rev. Lett., 105(6): 068101, 2010. Cf. aussi arXiv:1007.1871.
 | Cell Model Approach to Membrane Mediated Protein Interactions
Martin Michael Müller, Markus Deserno |
Résumé
Plus d'infos
Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.
 | Hamiltonian formulation of surfaces with constant Gaussian curvature
Miguel Trejo, Martine Ben Amar, Martin Michael Müller |
Résumé
Plus d'infos
J. Phys. A: Math. Theor., 42(42): 425204, 2009.
 | Local Membrane Mechanics of Pore-Spanning Bilayers
Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff |
The mechanical behavior of lipid bilayers spanning the pores of highly ordered porous silicon substrates was studied by local indentation experiments as a function of surface functionalization, lipid composition, solvent content, indentation velocity, and pore radius. Solvent-containing nanoblack lipid membranes (nano-BLMs) as well as solvent-free pore-spanning bilayers were imaged by fluorescence and atomic force microscopy prior to force curve acquisition, which allows distinguishing between membrane-covered and uncovered pores. Force indentation curves on pore-spanning bilayers attached to functionalized hydrophobic porous silicon substrates reveal a predominately linear response that is mainly attributed to prestress in the membranes. This is in agreement with the observation that indentation leads to membrane lysis well below 5% area dilatation. However, membrane bending and lateral tension dominates over
prestress and stretching if solvent-free supported membranes obtained from spreading giant liposomes on hydrophilic porous silicon are indented.
 Fermer
Plus d'infos Fermer
Plus d'infos
J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.
 | Elasticity Mapping of Pore-Suspending Native Cell Membranes
Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
Small, 5(7): pp. 832-838, 2009.
 | Conical Defects in Growing Sheets
Martin Michael Müller, Martine Ben Amar, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. Lett., 101(15): 156104, 2008. Cf. aussi arXiv:0807.1814.
 | How paper folds: bending with local constraints
Jemal Guven, Martin Michael Müller |
Résumé
Plus d'infos
J. Phys. A: Math. Theor., 41(5): 055203, 2008. Cf. aussi arXiv:0712.0978.
 | Contact lines for fluid surface adhesion
Markus Deserno, Martin Michael Müller, Jemal Guven |
When a fluid surface adheres to a substrate, the location of the
contact line adjusts in order to minimize the overall energy. This
adhesion balance implies boundary conditions which depend on the
characteristic surface deformation energies. We develop a general
geometrical framework within which these conditions can be
systematically derived.
We treat both adhesion to a rigid substrate as well as adhesion
between two fluid surfaces, and illustrate our general results for
several important Hamiltonians involving both curvature and
curvature gradients. Some of these have previously been studied
using very different techniques, others are to our knowledge new.
What becomes clear in our approach is that, except for capillary
phenomena, these boundary conditions are not the manifestation
of a local force balance, even if the concept of surface stress is
properly generalized. Hamiltonians containing higher order surface
derivatives are not just sensitive to boundary translations but also
notice changes in slope or even curvature.
Both the necessity and the functional form of the corresponding
additional contributions follow readily from our treatment.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. E, 76(1): 011605, 2007. Cf. aussi cond-mat/0703019.
 | Balancing torques in membrane-mediated interactions: Exact results and
numerical illustrations
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 76(1): 011921, 2007. Cf. aussi cond-mat/0702340.
 | Aggregation and vesiculation of membrane proteins by curvature-mediated
interactions
Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno |
Résumé
Plus d'infos
Nature 447(7143): pp. 461-464, 2007.
 | How to determine local elastic properties of lipid bilayer membranes
from atomic-force-microscope measurements: A theoretical analysis
Davood Norouzi, Martin Michael Müller, Markus Deserno |
Measurements with an atomic force microscope (AFM) offer a direct way to
probe elastic properties of lipid bilayer membranes locally: provided
the underlying stress-strain relation is known, material parameters such as
surface tension or bending rigidity may be deduced.
In a recent experiment a pore-spanning membrane was poked with an AFM tip,
yielding a linear behavior of the force-indentation curves. A theoretical
model for this case is presented here which describes these curves in the
framework of Helfrich theory. The linear behavior of the measurements is
reproduced if one neglects the influence of adhesion between tip and membrane.
Including it via an adhesion balance changes the situation significantly:
force-distance curves cease to be linear, hysteresis and nonzero detachment
forces can show up. The characteristics of this rich scenario are discussed
in detail in this article.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. E, 74(6): 061914, 2006. Cf. aussi cond-mat/0602662.
 | Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy
Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
Biophys. J., 91(1): pp. 217-226, 2006.
 | Interface mediated interactions between particles -- a geometrical approach
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 72(6): 061407, 2005. Cf. aussi cond-mat/0506019.
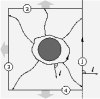 | Geometry of surface-mediated interactions
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Europhys. Lett., 69(3): pp. 482-488, 2005. Cf. aussi cond-mat/0409043.
2. Livres et ouvrages collectifs
3. Mémoires
-
Theoretical examinations of interface mediated interactions between colloidal particles,
mémoire (2004).
-
Theoretical studies of fluid membrane mechanics, thèse de doctorat (2007).
-
Symmetry breaking in bioelasticity, thèse d'habilitation à diriger des recherches (2015).
|


