Publications (en anglais)
-
Articles scientifiques
-
Livres et ouvrages collectifs
-
Mémoires
Voir aussi les profiles sur
Publons,
Orcid ou
Google Scholar.
1. Articles scientifiques
 | Protein-membrane interactions with a twist
Jordan Klein, Loréne Schad, Thérèse E. Malliavin, Martin Michael Müller |
Résumé
Soft Matter, 21: 4336, 2025.
 | Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic
Description of the Coiled-Coil Helix Bundle
Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller |
Résumé
Int. J. Mol. Sci., 25: 2481, 2024.
 | Flexoelectric fluid membrane vesicles in spherical confinement
Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller |
Résumé
Plus d'infos
EPL, 131(1): 18001, 2020. Cf. aussi arXiv:2006.04475.
 | Isometric bending requires local constraints on free edges
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Résumé
Plus d'infos
Math. Mech. Solids, 24: 4051, 2019. Cf. aussi arXiv:1904.05855.
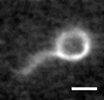 | Helical Superstructure of Intermediate Filaments
Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić |
Résumé
Plus d'infos
Phys. Rev. Lett., 122: 098101, 2019. Cf. aussi arXiv:1803.04691.
 | Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows
Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller |
Résumé
Phys. Rev. E, 98: 043111, 2018. Cf. aussi arXiv:1810.04500.
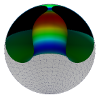 | Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Résumé
Plus d'infos
IOP Conf. Series: MSE, 186: 012021, 2017.
 | Squeezed helical elastica
Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach |
Résumé
Plus d'infos
Eur. Phys. J. E, 39: 114, 2016. Cf. aussi arXiv:1606.03611.
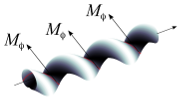 | How bio-filaments twist membranes
Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller |
Résumé
Soft Matter, 12: 5747, 2016.
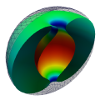 | Toroidal membrane vesicles in spherical confinement
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Résumé
Plus d'infos
Phys. Rev. E, 92: 032721, 2015. Cf. aussi arXiv:1509.00765.
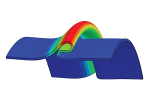 | Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate
Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
Int. J. Non-Linear Mech., 75: 115, 2015. Cf. aussi arXiv:1503.05030.
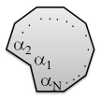 | Crunching Biofilament Rings
Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić |
Résumé
Plus d'infos
Europhys. Lett., 107(6): 68002, 2014. Cf. aussi arXiv:1408.6787.
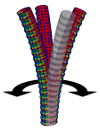 | Confotronic dynamics of tubular filaments
Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić |
Résumé
Plus d'infos
Soft Matter, 10(16): pp. 2836-2847, 2014. Cf. aussi arXiv:1312.3106.
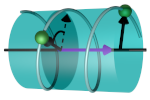
 | Whirling skirts and rotating cones
Jemal Guven, J. A. Hanna, Martin Michael Müller |
Steady, dihedrally symmetric patterns with sharp peaks may be observed on a spinning skirt, lagging behind the material flow of the fabric. These qualitative features are captured with a minimal model of traveling waves on an inextensible, flexible, generalized-conical sheet rotating about a fixed axis. Conservation laws are used to reduce the dynamics to a quadrature describing a particle in a three-parameter family of potentials. One parameter is associated with the stress in the sheet, aNoether is the current associated with rotational invariance, and the third is a Rossby number which indicates the relative strength of Coriolis forces. Solutions are quantized by enforcing a topology appropriate to a skirt and a particular choice of dihedral symmetry. A perturbative analysis of nearly axisymmetric cones shows that Coriolis effects are essential in establishing skirt-like solutions. Fully non-linear solutions with three-fold symmetry are presented which bear a suggestive resemblance to the observed patterns.
 Fermer Fermer
New J. Phys., 15: 113055, 2013. Cf. aussi arXiv:1306.2619.
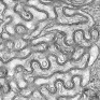 | Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo
Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte |
Résumé
J. Cell Sci., 126(8): 1806, 2013.
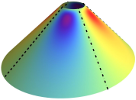
 | Dipoles in thin sheets
Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller |
A flat elastic sheet may contain pointlike conical singularities that carry a metrical "charge" of Gaussian curvature. Adding such elementary defects to a sheet allows one to make many shapes, in a manner broadly
analogous to the familiar multipole construction in electrostatics. However, here the underlying field theory is non-linear,
and superposition of intrinsic defects is non-trivial as it must respect the immersion of the resulting surface in three
dimensions. We consider a "charge-neutral" dipole composed of two conical singularities of opposite sign.
Unlike the relatively simple electrostatic case, here there are two distinct stable minima and an infinity of unstable equilibria.
We determine the shapes of the minima and evaluate their energies in the thin-sheet regime where bending dominates
over stretching. Our predictions are in surprisingly good agreement with experiments on paper sheets.
 Fermer
Plus d'infos Fermer
Plus d'infos
Eur. Phys. J. E, 36: 106, 2013. Cf. aussi arXiv:1212.3262.
 | Fluid membrane vesicles in confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
We numerically study the morphology of fluid membrane vesicles with prescribed volume and surface area in confinement.
For spherical confinement we observe axisymmetric invaginations that transform into ellipsoidal invaginations a the area of the
vesicle is increased, followed by a transition into stomatocyte-like shapes.
We provide a detailed analysis of the axisymmetric shapes and investigate the effect of the spontaneous curvature of the membrane
as a possible mechanism for shape regulation. We show that the observed morphologies are stable under small geometric deformations
of the confinement. The results could help to understand the role of mechanics in the complex folding patterns of biological membranes.
 Fermer
Plus d'infos Fermer
Plus d'infos
New J. Phys., 14: 095021, 2012.
 | Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity
Martine Ben Amar, Martin Michael Müller, Miguel Trejo |
Résumé
Plus d'infos
New J. Phys., 14: 085014, 2012. Choisi pour les Highlights of 2012.
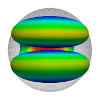
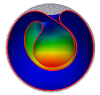 | Morphogenesis of membrane invaginations in spherical confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
Europhys. Lett., 97(6): 68008, 2012. Cf. aussi arXiv:1201.2518.
 | Conical instabilities on paper
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
The stability of the fundamental defects of an unstretchable flat sheet is examined.
This involves expanding the bending energy to second order in deformations about the
defect. The modes of deformation occur as eigenstates of a fourth-order linear differential
operator. Unstretchability places a global linear constraint on these modes. Conical
defects with a surplus angle exhibit an infinite number of states. If this angle is below a
critical value, these states possess an n-fold symmetry labeled by an integer, n ≥ 2. A
nonlinear stability analysis shows that the 2-fold ground state is stable, whereas excited
states possess 2(n - 2) unstable modes which come in even and odd pairs.
 Fermer
Plus d'infos Fermer
Plus d'infos
J. Phys. A: Math. Theor., 45(1): 015203, 2012. Cf. aussi arXiv:1107.5008.
 | Interface-mediated interactions: Entropic forces of curved membranes
Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller |
Particles embedded in a fluctuating interface experience forces and torques
mediated by the deformations and by the thermal fluctuations of the medium.
Considering a system of two cylinders bound to a fluid membrane we show that
the entropic contribution enhances the curvature-mediated repulsion between
the two cylinders. This is contrary to the usual attractive Casimir force in
the absence of curvature-mediated interactions. For a large distance between
the cylinders, we retrieve the renormalization of the surface tension of a
flat membrane due to thermal fluctuations.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. E, 83(5): 051921, 2011. Cf. aussi arXiv:1011.1221.
 | Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann |
We investigate the morphology of thin discs and rings growing in circumferential direction. Recent analytical results suggest that this growth produces symmetric excess cones (e-cones). We study the stability of such solutions considering self-contact and bending stress. We show that, contrary to what was assumed in previous analytical solutions, beyond a critical growth factor, no symmetric e-cone solution is energetically minimal any more. Instead, we obtain skewed e-cone solutions having lower energy, characterized by a skewness angle and repetitive spiral winding with increasing growth. These results are generalized to discs with varying thickness and rings with holes of different radii.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. Lett., 105(6): 068101, 2010. Cf. aussi arXiv:1007.1871.
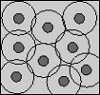 | Cell Model Approach to Membrane Mediated Protein Interactions
Martin Michael Müller, Markus Deserno |
Résumé
Plus d'infos
Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.
 | Hamiltonian formulation of surfaces with constant Gaussian curvature
Miguel Trejo, Martine Ben Amar, Martin Michael Müller |
Résumé
Plus d'infos
J. Phys. A: Math. Theor., 42(42): 425204, 2009.
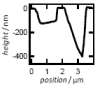 | Local Membrane Mechanics of Pore-Spanning Bilayers
Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.
 | Elasticity Mapping of Pore-Suspending Native Cell Membranes
Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
Small, 5(7): pp. 832-838, 2009.
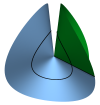 | Conical Defects in Growing Sheets
Martin Michael Müller, Martine Ben Amar, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. Lett., 101(15): 156104, 2008. Cf. aussi arXiv:0807.1814.
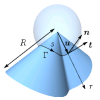 | How paper folds: bending with local constraints
Jemal Guven, Martin Michael Müller |
Résumé
Plus d'infos
J. Phys. A: Math. Theor., 41(5): 055203, 2008. Cf. aussi arXiv:0712.0978.
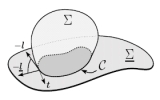 | Contact lines for fluid surface adhesion
Markus Deserno, Martin Michael Müller, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 76(1): 011605, 2007. Cf. aussi cond-mat/0703019.
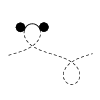 | Balancing torques in membrane-mediated interactions: Exact results and
numerical illustrations
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 76(1): 011921, 2007. Cf. aussi cond-mat/0702340.
 | Aggregation and vesiculation of membrane proteins by curvature-mediated
interactions
Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno |
Résumé
Plus d'infos
Nature 447(7143): pp. 461-464, 2007.
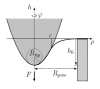 | How to determine local elastic properties of lipid bilayer membranes
from atomic-force-microscope measurements: A theoretical analysis
Davood Norouzi, Martin Michael Müller, Markus Deserno |
Résumé
Plus d'infos
Phys. Rev. E, 74(6): 061914, 2006. Cf. aussi cond-mat/0602662.
 | Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy
Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
Biophys. J., 91(1): pp. 217-226, 2006.
 | Interface mediated interactions between particles -- a geometrical approach
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 72(6): 061407, 2005. Cf. aussi cond-mat/0506019.
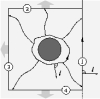 | Geometry of surface-mediated interactions
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Europhys. Lett., 69(3): pp. 482-488, 2005. Cf. aussi cond-mat/0409043.
2. Livres et ouvrages collectifs
3. Mémoires
-
Theoretical examinations of interface mediated interactions between colloidal particles,
mémoire (2004).
-
Theoretical studies of fluid membrane mechanics, thèse de doctorat (2007).
-
Symmetry breaking in bioelasticity, thèse d'habilitation à diriger des recherches (2015).
|


