Publications (en anglais)
-
Articles scientifiques
-
Livres et ouvrages collectifs
-
Mémoires
Voir aussi les profiles sur
Publons,
Orcid ou
Google Scholar.
1. Articles scientifiques
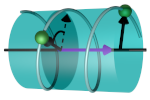
 | Protein-membrane interactions with a twist
Jordan Klein, Loréne Schad, Thérèse E. Malliavin, Martin Michael Müller |
Résumé
Soft Matter, 21: 4336, 2025.
 | Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic
Description of the Coiled-Coil Helix Bundle
Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller |
Résumé
Int. J. Mol. Sci., 25: 2481, 2024.
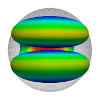 | Flexoelectric fluid membrane vesicles in spherical confinement
Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller |
Résumé
Plus d'infos
EPL, 131(1): 18001, 2020. Cf. aussi arXiv:2006.04475.
 | Isometric bending requires local constraints on free edges
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Résumé
Plus d'infos
Math. Mech. Solids, 24: 4051, 2019. Cf. aussi arXiv:1904.05855.
 | Helical Superstructure of Intermediate Filaments
Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić |
Intermediate filaments are the least explored among the large cytoskeletal elements.
We show here that they display conformational anomalies in narrow microfluidic channels.
Their unusual behavior can be understood as the consequence of a previously undetected, large scale
helically curved superstructure. Confinement in a channel orders the otherwise soft, strongly
fluctuating helical filaments and enhances their structural correlations, giving rise to experimentally
detectable, strongly oscillating tangent correlation functions. We propose an explanation for the detected
intrinsic curving phenomenon - an elastic shape instability that we call autocoiling. The mechanism
involves self-induced filament buckling via a surface stress located at the outside of the
cross-section. The results agree with ultrastructural findings and rationalize for the commonly observed
looped intermediate filament shapes. Beyond curvature, explaining the molecular origin of the detected helical
torsion remains an interesting challenge.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. Lett., 122: 098101, 2019. Cf. aussi arXiv:1803.04691.
 | Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows
Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller |
We present a numerical study of the time-dependent motion of a membrane vesicle in a
channel under an imposed flow. In a Poiseuille flow the shape of the vesicle depends on the flow strength,
the mechanical properties of the membrane, and the width of the channel. In a wide parameter region, the
emerging snaking shape shows an oscillatory motion like a swimmer flagella even though the flow is
stationary. We quantify this behavior by the amplitude and frequency of the oscillations of the vesicle's
center of mass. The influence of an amplitude modulation of the imposed flow on the dynamics and shape of
the snaking vesicle is also investigated. We find that this modulation---when sufficiently small---induces
a modulation in amplitude and frequency of the center of mass of the snaking vesicle. For large
modulation amplitudes transitions to static shapes are observed.
 Fermer Fermer
Phys. Rev. E, 98: 043111, 2018. Cf. aussi arXiv:1810.04500.
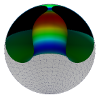 | Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Résumé
Plus d'infos
IOP Conf. Series: MSE, 186: 012021, 2017.
 | Squeezed helical elastica
Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach |
Résumé
Plus d'infos
Eur. Phys. J. E, 39: 114, 2016. Cf. aussi arXiv:1606.03611.
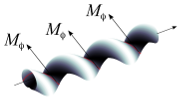 | How bio-filaments twist membranes
Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller |
We study the deformations of a fluid membrane imposed by adhering stiff
bio-filaments due to the torques they apply. In the limit of small deformations, we
derive a general expression for the energy and the deformation field of the membrane.
This expression is specialised to different important cases including closed and helical
bio-filaments. In particular, we analyse interface-mediated interactions and membrane
wrapping when the filaments apply a local torque distribution on a tubular membrane.
 Fermer Fermer
Soft Matter, 12: 5747, 2016.
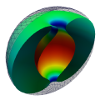 | Toroidal membrane vesicles in spherical confinement
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
We investigate the morphology of a toroidal fluid membrane vesicle confined inside a spherical container.
The equilibrium shapes are assembled in a geometrical phase diagram as a function of scaled area and
reduced volume of the membrane. For small area the vesicle can adopt its free form. When increasing
the area, the membrane cannot avoid contact and touches the confining sphere along a circular contact line,
which extends to a zone of contact for higher area. The elastic energies of the equilibrium shapes are
compared to those of their confined counterparts of spherical topology to predict under which conditions a
topology change is favored energetically.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. E, 92: 032721, 2015. Cf. aussi arXiv:1509.00765.
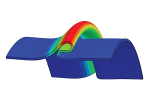 | Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate
Norbert Stoop, Martin Michael Müller |
We consider the axial compression of a thin sheet wrapped around a rigid cylindrical substrate. In contrast to the wrinkling-to-fold transitions exhibited in similar systems, we find that the sheet always buckles into a single symmetric fold, while periodic solutions are unstable. Upon further compression, the solution breaks symmetry and stabilizes into a recumbent fold. Using linear analysis and numerics, we theoretically predict the buckling force and energy as a function of the compressive displacement. We compare our theory to experiments employing cylindrical neoprene sheets and find remarkably good agreement.
 Fermer
Plus d'infos Fermer
Plus d'infos
Int. J. Non-Linear Mech., 75: 115, 2015. Cf. aussi arXiv:1503.05030.
 | Crunching Biofilament Rings
Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić |
Résumé
Plus d'infos
Europhys. Lett., 107(6): 68002, 2014. Cf. aussi arXiv:1408.6787.
 | Confotronic dynamics of tubular filaments
Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić |
Résumé
Plus d'infos
Soft Matter, 10(16): pp. 2836-2847, 2014. Cf. aussi arXiv:1312.3106.
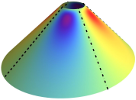
 | Whirling skirts and rotating cones
Jemal Guven, J. A. Hanna, Martin Michael Müller |
Résumé
New J. Phys., 15: 113055, 2013. Cf. aussi arXiv:1306.2619.
 | Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo
Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte |
Résumé
J. Cell Sci., 126(8): 1806, 2013.
 | Dipoles in thin sheets
Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller |
Résumé
Plus d'infos
Eur. Phys. J. E, 36: 106, 2013. Cf. aussi arXiv:1212.3262.
 | Fluid membrane vesicles in confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
New J. Phys., 14: 095021, 2012.
 | Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity
Martine Ben Amar, Martin Michael Müller, Miguel Trejo |
Résumé
Plus d'infos
New J. Phys., 14: 085014, 2012. Choisi pour les Highlights of 2012.
 | Morphogenesis of membrane invaginations in spherical confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Résumé
Plus d'infos
Europhys. Lett., 97(6): 68008, 2012. Cf. aussi arXiv:1201.2518.
 | Conical instabilities on paper
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Résumé
Plus d'infos
J. Phys. A: Math. Theor., 45(1): 015203, 2012. Cf. aussi arXiv:1107.5008.
 | Interface-mediated interactions: Entropic forces of curved membranes
Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller |
Résumé
Plus d'infos
Phys. Rev. E, 83(5): 051921, 2011. Cf. aussi arXiv:1011.1221.
 | Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann |
Résumé
Plus d'infos
Phys. Rev. Lett., 105(6): 068101, 2010. Cf. aussi arXiv:1007.1871.
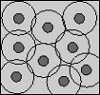 | Cell Model Approach to Membrane Mediated Protein Interactions
Martin Michael Müller, Markus Deserno |
Résumé
Plus d'infos
Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.
 | Hamiltonian formulation of surfaces with constant Gaussian curvature
Miguel Trejo, Martine Ben Amar, Martin Michael Müller |
Dirac's method for constrained Hamiltonian systems is used to describe surfaces of constant Gaussian curvature. A geometrical free energy, for which these surfaces are equilibrium states, is introduced and interpreted as an action. An equilibrium surface can then be generated by the evolution of a closed space curve.
Since the underlying action depends on second derivatives, the velocity of the curve and its conjugate momentum must be included in the set of phase space variables. Furthermore, the action is linear in the acceleration of the curve and possesses a local symmetry---reparametrization invariance---which implies primary constraints in the canonical formalism. These constraints are incorporated into the Hamiltonian through Lagrange multiplier functions, that are identified as the components of the acceleration of the curve. The formulation leads to four first order partial differential equations, one for each canonical variable.
With the appropriate choice of parametrization only one of these equations has to be solved to obtain the surface which is swept out by the evolving space curve. To illustrate the formalism, several evolutions of pseudospherical surfaces are discussed.
 Fermer
Plus d'infos Fermer
Plus d'infos
J. Phys. A: Math. Theor., 42(42): 425204, 2009.
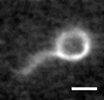
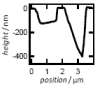 | Local Membrane Mechanics of Pore-Spanning Bilayers
Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.
 | Elasticity Mapping of Pore-Suspending Native Cell Membranes
Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
Small, 5(7): pp. 832-838, 2009.
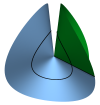 | Conical Defects in Growing Sheets
Martin Michael Müller, Martine Ben Amar, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. Lett., 101(15): 156104, 2008. Cf. aussi arXiv:0807.1814.
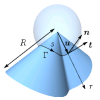 | How paper folds: bending with local constraints
Jemal Guven, Martin Michael Müller |
A variational framework is introduced to describe how a surface bends when it is subject to local constraints on its geometry. This framework is applied to describe the patterns of a folded sheet of paper. The unstretchability of paper implies a constraint on the surface metric; bending is penalized by an energy quadratic in mean curvature. The local Lagrange multipliers enforcing the constraint are identified with a conserved tangential stress that couples to the extrinsic curvature of the sheet. The framework is illustrated by examining the deformation of a flat sheet into a generalized cone.
 Fermer
Plus d'infos Fermer
Plus d'infos
J. Phys. A: Math. Theor., 41(5): 055203, 2008. Cf. aussi arXiv:0712.0978.
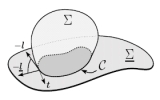 | Contact lines for fluid surface adhesion
Markus Deserno, Martin Michael Müller, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 76(1): 011605, 2007. Cf. aussi cond-mat/0703019.
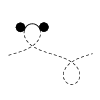 | Balancing torques in membrane-mediated interactions: Exact results and
numerical illustrations
Martin Michael Müller, Markus Deserno, Jemal Guven |
Torques on interfaces can be described by a divergence-free tensor
which is fully encoded in the geometry. This tensor consists of two
terms, one originating in the couple of the stress, the other capturing
an intrinsic contribution due to curvature. In analogy to the description
of forces in terms of a stress tensor, the torque on a particle can be
expressed as a line integral along any contour surrounding the particle.
Interactions between particles mediated by a fluid membrane are studied
within this framework. In particular, torque balance places a strong
constraint on the shape of the membrane. Symmetric two-particle
configurations admit simple analytical expressions which are valid
in the fully nonlinear regime; in particular, the problem may be
solved exactly in the case of two membrane-bound parallel cylinders.
This apparently simple system provides some flavor of the remarkably
subtle nonlinear behavior associated with membrane-mediated interactions.
 Fermer
Plus d'infos Fermer
Plus d'infos
Phys. Rev. E, 76(1): 011921, 2007. Cf. aussi cond-mat/0702340.
 | Aggregation and vesiculation of membrane proteins by curvature-mediated
interactions
Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno |
Résumé
Plus d'infos
Nature 447(7143): pp. 461-464, 2007.
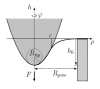 | How to determine local elastic properties of lipid bilayer membranes
from atomic-force-microscope measurements: A theoretical analysis
Davood Norouzi, Martin Michael Müller, Markus Deserno |
Résumé
Plus d'infos
Phys. Rev. E, 74(6): 061914, 2006. Cf. aussi cond-mat/0602662.
 | Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy
Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff |
Résumé
Plus d'infos
Biophys. J., 91(1): pp. 217-226, 2006.
 | Interface mediated interactions between particles -- a geometrical approach
Martin Michael Müller, Markus Deserno, Jemal Guven |
Résumé
Plus d'infos
Phys. Rev. E, 72(6): 061407, 2005. Cf. aussi cond-mat/0506019.
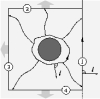 | Geometry of surface-mediated interactions
Martin Michael Müller, Markus Deserno, Jemal Guven |
Soft interfaces can mediate interactions between particles bound to
them. The force transmitted through the surface geometry on a
particle may be expressed as a closed line integral of the surface
stress tensor around that particle. This contour may be deformed to
exploit the symmetries present; for two identical particles, one
obtains an exact expression for the force between them in terms of
the local surface geometry of their mid-plane; in the case of a
fluid membrane the sign of the interaction is often evident. The
approach, by construction, is adapted directly to the surface and is
independent of its parameterization. Furthermore, it is applicable
for arbitrarily large deformations; in particular, it remains valid
beyond the linear small-gradient regime.
 Fermer
Plus d'infos Fermer
Plus d'infos
Europhys. Lett., 69(3): pp. 482-488, 2005. Cf. aussi cond-mat/0409043.
2. Livres et ouvrages collectifs
3. Mémoires
-
Theoretical examinations of interface mediated interactions between colloidal particles,
mémoire (2004).
-
Theoretical studies of fluid membrane mechanics, thèse de doctorat (2007).
-
Symmetry breaking in bioelasticity, thèse d'habilitation à diriger des recherches (2015).
|


