Publications
-
Articles in scientific journals
-
Books and collective works
-
Theses
See also profiles on Publons,
Orcid or
Google Scholar.
1. Articles in scientific journals
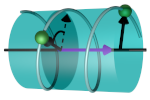
 | Protein-membrane interactions with a twist
Jordan Klein, Loréne Schad, Thérèse E. Malliavin, Martin Michael Müller |
Abstract
Soft Matter, 21: 4336, 2025.
 | Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic
Description of the Coiled-Coil Helix Bundle
Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller |
Abstract
Int. J. Mol. Sci., 25: 2481, 2024.
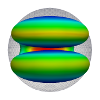 | Flexoelectric fluid membrane vesicles in spherical confinement
Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller |
Abstract
Read more
EPL, 131(1): 18001, 2020. See also arXiv:2006.04475.
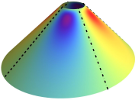 | Isometric bending requires local constraints on free edges
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
While the shape equations describing the equilibrium of an unstretchable thin sheet that is free
to bend are known, the boundary conditions that supplement these equations on free edges have remained elusive.
Intuitively, unstretchability is captured by a constraint on the metric within the bulk. Naïvely one would then
guess that this constraint is enough to ensure that the deformations determining the boundary conditions on these
edges respect the isometry constraint. If matters were this simple, unfortunately, it would imply unbalanced torques
(as well as forces) along the edge unless manifestly unphysical constraints are met by the boundary geometry. In this
article, we identify the source of the problem: not only the local arc-length but also the geodesic curvature need to
be constrained explicitly on all free edges. We derive the boundary conditions which follow. In contrast to conventional
wisdom, there is no need to introduce boundary layers. This framework is applied to isolated conical defects, both
with deficit as well, but more briefly, as surplus angles. Using these boundary conditions, we show that the lateral
tension within a circular cone of fixed radius is equal but opposite to the radial compression, and independent of
the deficit angle itself. We proceed to examine the effect of an oblique outer edge on this cone perturbatively
demonstrating that both the correction to the geometry as well as the stress distribution in the cone kicks in at
second order in the eccentricity of the edge.
 Reduce
Read more Reduce
Read more
Math. Mech. Solids, 24: 4051, 2019. See also arXiv:1904.05855.
 | Helical Superstructure of Intermediate Filaments
Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić |
Abstract
Read more
Phys. Rev. Lett., 122: 098101, 2019. See also arXiv:1803.04691.
 | Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows
Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller |
Abstract
Phys. Rev. E, 98: 043111, 2018. See also arXiv:1810.04500.
 | Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Abstract
Read more
IOP Conf. Series: MSE, 186: 012021, 2017.
 | Squeezed helical elastica
Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach |
Abstract
Read more
Eur. Phys. J. E, 39: 114, 2016. See also arXiv:1606.03611.
 | How bio-filaments twist membranes
Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller |
Abstract
Soft Matter, 12: 5747, 2016.
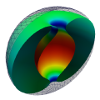 | Toroidal membrane vesicles in spherical confinement
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
We investigate the morphology of a toroidal fluid membrane vesicle confined inside a spherical container.
The equilibrium shapes are assembled in a geometrical phase diagram as a function of scaled area and
reduced volume of the membrane. For small area the vesicle can adopt its free form. When increasing
the area, the membrane cannot avoid contact and touches the confining sphere along a circular contact line,
which extends to a zone of contact for higher area. The elastic energies of the equilibrium shapes are
compared to those of their confined counterparts of spherical topology to predict under which conditions a
topology change is favored energetically.
 Reduce
Read more Reduce
Read more
Phys. Rev. E, 92: 032721, 2015. See also arXiv:1509.00765.
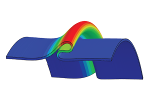 | Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate
Norbert Stoop, Martin Michael Müller |
Abstract
Read more
Int. J. Non-Linear Mech., 75: 115, 2015. See also arXiv:1503.05030.
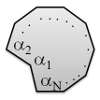 | Crunching Biofilament Rings
Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić |
Abstract
Read more
Europhys. Lett., 107(6): 68002, 2014. See also arXiv:1408.6787.
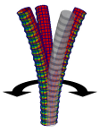 | Confotronic dynamics of tubular filaments
Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić |
Abstract
Read more
Soft Matter, 10(16): pp. 2836-2847, 2014. See also arXiv:1312.3106.
 | Whirling skirts and rotating cones
Jemal Guven, J. A. Hanna, Martin Michael Müller |
Steady, dihedrally symmetric patterns with sharp peaks may be observed on a spinning skirt, lagging behind the material flow of the fabric. These qualitative features are captured with a minimal model of traveling waves on an inextensible, flexible, generalized-conical sheet rotating about a fixed axis. Conservation laws are used to reduce the dynamics to a quadrature describing a particle in a three-parameter family of potentials. One parameter is associated with the stress in the sheet, aNoether is the current associated with rotational invariance, and the third is a Rossby number which indicates the relative strength of Coriolis forces. Solutions are quantized by enforcing a topology appropriate to a skirt and a particular choice of dihedral symmetry. A perturbative analysis of nearly axisymmetric cones shows that Coriolis effects are essential in establishing skirt-like solutions. Fully non-linear solutions with three-fold symmetry are presented which bear a suggestive resemblance to the observed patterns.
 Reduce Reduce
New J. Phys., 15: 113055, 2013. See also arXiv:1306.2619.
 | Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo
Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte |
Abstract
J. Cell Sci., 126(8): 1806, 2013.
 | Dipoles in thin sheets
Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller |
Abstract
Read more
Eur. Phys. J. E, 36: 106, 2013. See also arXiv:1212.3262.
 | Fluid membrane vesicles in confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Abstract
Read more
New J. Phys., 14: 095021, 2012.
 | Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity
Martine Ben Amar, Martin Michael Müller, Miguel Trejo |
The growth of a thin elastic sheet imposes constraints on its geometry such as its Gaussian curvature KG.
In this paper, we construct the shapes of sympetalous bell-shaped flowers with a constant Gaussian curvature. Minimizing the bending energies
of both the petal and the veins, we are able to predict quantitatively the global shape of these flowers. We discuss two toy problems
where the Gaussian curvature is either negative or positive. In the former case the axisymmetric pseudosphere turns out to mimic the correct
shape before edge curling; in the latter case, singularities of the mathematical surface coincide with strong veins. Using a variational
minimization of the elastic energy, we find that the optimal number for the veins is either four, five or six, a number which is deceptively
close to the statistics on real flowers in nature.
 Reduce
Read more Reduce
Read more
New J. Phys., 14: 085014, 2012. Also featured in the Highlights of 2012.
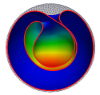 | Morphogenesis of membrane invaginations in spherical confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Abstract
Read more
Europhys. Lett., 97(6): 68008, 2012. See also arXiv:1201.2518.
 | Conical instabilities on paper
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Abstract
Read more
J. Phys. A: Math. Theor., 45(1): 015203, 2012. See also arXiv:1107.5008.
 | Interface-mediated interactions: Entropic forces of curved membranes
Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller |
Abstract
Read more
Phys. Rev. E, 83(5): 051921, 2011. See also arXiv:1011.1221.
 | Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann |
We investigate the morphology of thin discs and rings growing in circumferential direction. Recent analytical results suggest that this growth produces symmetric excess cones (e-cones). We study the stability of such solutions considering self-contact and bending stress. We show that, contrary to what was assumed in previous analytical solutions, beyond a critical growth factor, no symmetric e-cone solution is energetically minimal any more. Instead, we obtain skewed e-cone solutions having lower energy, characterized by a skewness angle and repetitive spiral winding with increasing growth. These results are generalized to discs with varying thickness and rings with holes of different radii.
 Reduce
Read more Reduce
Read more
Phys. Rev. Lett., 105(6): 068101, 2010. See also arXiv:1007.1871.
 | Cell Model Approach to Membrane Mediated Protein Interactions
Martin Michael Müller, Markus Deserno |
Abstract
Read more
Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.
 | Hamiltonian formulation of surfaces with constant Gaussian curvature
Miguel Trejo, Martine Ben Amar, Martin Michael Müller |
Dirac's method for constrained Hamiltonian systems is used to describe surfaces of constant Gaussian curvature. A geometrical free energy, for which these surfaces are equilibrium states, is introduced and interpreted as an action. An equilibrium surface can then be generated by the evolution of a closed space curve.
Since the underlying action depends on second derivatives, the velocity of the curve and its conjugate momentum must be included in the set of phase space variables. Furthermore, the action is linear in the acceleration of the curve and possesses a local symmetry---reparametrization invariance---which implies primary constraints in the canonical formalism. These constraints are incorporated into the Hamiltonian through Lagrange multiplier functions, that are identified as the components of the acceleration of the curve. The formulation leads to four first order partial differential equations, one for each canonical variable.
With the appropriate choice of parametrization only one of these equations has to be solved to obtain the surface which is swept out by the evolving space curve. To illustrate the formalism, several evolutions of pseudospherical surfaces are discussed.
 Reduce
Read more Reduce
Read more
J. Phys. A: Math. Theor., 42(42): 425204, 2009.
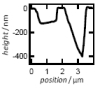 | Local Membrane Mechanics of Pore-Spanning Bilayers
Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.
 | Elasticity Mapping of Pore-Suspending Native Cell Membranes
Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
Small, 5(7): pp. 832-838, 2009.
 | Conical Defects in Growing Sheets
Martin Michael Müller, Martine Ben Amar, Jemal Guven |
A growing or shrinking disc will adopt a conical shape, its intrinsic geometry characterized by a surplus angle φe at the apex. If growth is slow, the cone will find its equilibrium. Whereas this is trivial if φe≤0, the disc can fold into one of a discrete infinite number of states if φe is positive. We construct these states in the regime where bending dominates, determine their energies and how stress is distributed in them. For each state a critical value of φe is identified beyond which the cone touches itself. Before this occurs, all states are stable; the ground state has twofold symmetry.
 Reduce
Read more Reduce
Read more
Phys. Rev. Lett., 101(15): 156104, 2008. See also arXiv:0807.1814.
 | How paper folds: bending with local constraints
Jemal Guven, Martin Michael Müller |
Abstract
Read more
J. Phys. A: Math. Theor., 41(5): 055203, 2008. See also arXiv:0712.0978.
 | Contact lines for fluid surface adhesion
Markus Deserno, Martin Michael Müller, Jemal Guven |
Abstract
Read more
Phys. Rev. E, 76(1): 011605, 2007. See also cond-mat/0703019.
 | Balancing torques in membrane-mediated interactions: Exact results and
numerical illustrations
Martin Michael Müller, Markus Deserno, Jemal Guven |
Abstract
Read more
Phys. Rev. E, 76(1): 011921, 2007. See also cond-mat/0702340.
 | Aggregation and vesiculation of membrane proteins by curvature-mediated
interactions
Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno |
Abstract
Read more
Nature 447(7143): pp. 461-464, 2007.
 | How to determine local elastic properties of lipid bilayer membranes
from atomic-force-microscope measurements: A theoretical analysis
Davood Norouzi, Martin Michael Müller, Markus Deserno |
Abstract
Read more
Phys. Rev. E, 74(6): 061914, 2006. See also cond-mat/0602662.
 | Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy
Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
Biophys. J., 91(1): pp. 217-226, 2006.
 | Interface mediated interactions between particles -- a geometrical approach
Martin Michael Müller, Markus Deserno, Jemal Guven |
Particles bound to an interface interact because they deform its shape.
The stresses that result are fully encoded in the geometry and described
by a divergence-free surface stress tensor. This stress tensor can be
used to express the force on a particle as a line integral along any
conveniently chosen closed contour that surrounds the particle. The
resulting expression is exact (i.e., free of any 'smallness' assumptions)
and independent of the chosen surface parametrization. Additional surface
degrees of freedom, such as vector fields describing lipid tilt, are readily
included in this formalism. As an illustration, we derive the exact force
for several important surface Hamiltonians in various symmetric two-particle
configurations in terms of the midplane geometry; its sign is evident in
certain interesting limits. Specializing to the linear regime, where the
shape can be analytically determined, these general expressions yield
force-distance relations, several of which have originally been derived
by using an energy based approach.
 Reduce
Read more Reduce
Read more
Phys. Rev. E, 72(6): 061407, 2005. See also cond-mat/0506019.
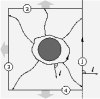 | Geometry of surface-mediated interactions
Martin Michael Müller, Markus Deserno, Jemal Guven |
Abstract
Read more
Europhys. Lett., 69(3): pp. 482-488, 2005. See also cond-mat/0409043.
2. Books and collective works
3. Theses
-
Theoretical examinations of interface mediated interactions between colloidal particles,
diploma thesis (2004).
-
Theoretical studies of fluid membrane mechanics, dissertation (2007).
-
Symmetry breaking in bioelasticity, habilitation thesis (2015).
|


