Publications
-
Articles in scientific journals
-
Books and collective works
-
Theses
See also profiles on Publons,
Orcid or
Google Scholar.
1. Articles in scientific journals
 | Protein-membrane interactions with a twist
Jordan Klein, Loréne Schad, Thérèse E. Malliavin, Martin Michael Müller |
Abstract
Soft Matter, 21: 4336, 2025.
 | Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic
Description of the Coiled-Coil Helix Bundle
Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller |
Abstract
Int. J. Mol. Sci., 25: 2481, 2024.
 | Flexoelectric fluid membrane vesicles in spherical confinement
Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller |
EPL, 131(1): 18001, 2020. See also arXiv:2006.04475.
 | Isometric bending requires local constraints on free edges
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Math. Mech. Solids, 24: 4051, 2019. See also arXiv:1904.05855.
 | Helical Superstructure of Intermediate Filaments
Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić |
Abstract
Read more
Phys. Rev. Lett., 122: 098101, 2019. See also arXiv:1803.04691.
 | Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows
Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller |
Abstract
Phys. Rev. E, 98: 043111, 2018. See also arXiv:1810.04500.
 | Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
We discuss how the equilibrium shapes of a confined toroidal fluid membrane vesicle
change when an adhesion between membrane and confining sphere is taken into account. The case without adhesion
was studied in Ref. [1]. Different types of solution were found and assembled in a phase diagram as a function of area
and reduced volume of the membrane. Depending on the degree of confinement the vesicle is either free, in contact along
a circle (contact-circle solutions) or on a surface (contact-area solutions). All solutions without adhesion are up-down symmetric.
When the container is adhesive, the phase diagram is altered and new kinds of solution without up-down symmetry are found.
For increasing values of adhesion the region of contact-circle solutions shrinks until it vanishes completely from the phase diagram.
 Reduce
Read more Reduce
Read more
IOP Conf. Series: MSE, 186: 012021, 2017.
 | Squeezed helical elastica
Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach |
We theoretically study the conformations of a helical semi-flexible filament
confined to a two-dimensional surface. This squeezed helix exhibits a variety of unexpected shapes
resembling circles, waves or spirals depending on the material parameters. We explore the conformation
space in detail and show that the shapes can be understood as the mutual elastic interaction of
conformational quasi-particles. Our theoretical results are potentially useful to
determine the material parameters of such helical filaments in an experimental setting.
 Reduce
Read more Reduce
Read more
Eur. Phys. J. E, 39: 114, 2016. See also arXiv:1606.03611.
 | How bio-filaments twist membranes
Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller |
Abstract
Soft Matter, 12: 5747, 2016.
 | Toroidal membrane vesicles in spherical confinement
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Abstract
Read more
Phys. Rev. E, 92: 032721, 2015. See also arXiv:1509.00765.
 | Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate
Norbert Stoop, Martin Michael Müller |
Abstract
Read more
Int. J. Non-Linear Mech., 75: 115, 2015. See also arXiv:1503.05030.
 | Crunching Biofilament Rings
Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić |
We discuss a curious example for the collective mechanical behavior of coupled non-linear monomer units entrapped in a circular filament. Within a simple model we elucidate how multistability of monomer units and exponentially large degeneracy of the filament's ground state emerge as a collective feature of the closed filament. Surprisingly, increasing the monomer frustration, i.e., the bending prestrain within the circular filament, leads to a conformational softening of the system. The phenomenon, that we term polymorphic crunching, is discussed and applied to a possible scenario for membrane tube deformation by switchable dynamin or FtsZ filaments. We find an important role of cooperative inter-unit interaction for efficient ring induced membrane fission.
 Reduce
Read more Reduce
Read more
Europhys. Lett., 107(6): 68002, 2014. See also arXiv:1408.6787.
 | Confotronic dynamics of tubular filaments
Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić |
Abstract
Read more
Soft Matter, 10(16): pp. 2836-2847, 2014. See also arXiv:1312.3106.
 | Whirling skirts and rotating cones
Jemal Guven, J. A. Hanna, Martin Michael Müller |
Abstract
New J. Phys., 15: 113055, 2013. See also arXiv:1306.2619.
 | Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo
Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte |
Abstract
J. Cell Sci., 126(8): 1806, 2013.
 | Dipoles in thin sheets
Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller |
Abstract
Read more
Eur. Phys. J. E, 36: 106, 2013. See also arXiv:1212.3262.
 | Fluid membrane vesicles in confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Abstract
Read more
New J. Phys., 14: 095021, 2012.
 | Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity
Martine Ben Amar, Martin Michael Müller, Miguel Trejo |
The growth of a thin elastic sheet imposes constraints on its geometry such as its Gaussian curvature KG.
In this paper, we construct the shapes of sympetalous bell-shaped flowers with a constant Gaussian curvature. Minimizing the bending energies
of both the petal and the veins, we are able to predict quantitatively the global shape of these flowers. We discuss two toy problems
where the Gaussian curvature is either negative or positive. In the former case the axisymmetric pseudosphere turns out to mimic the correct
shape before edge curling; in the latter case, singularities of the mathematical surface coincide with strong veins. Using a variational
minimization of the elastic energy, we find that the optimal number for the veins is either four, five or six, a number which is deceptively
close to the statistics on real flowers in nature.
 Reduce
Read more Reduce
Read more
New J. Phys., 14: 085014, 2012. Also featured in the Highlights of 2012.
 | Morphogenesis of membrane invaginations in spherical confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Abstract
Read more
Europhys. Lett., 97(6): 68008, 2012. See also arXiv:1201.2518.
 | Conical instabilities on paper
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Abstract
Read more
J. Phys. A: Math. Theor., 45(1): 015203, 2012. See also arXiv:1107.5008.
 | Interface-mediated interactions: Entropic forces of curved membranes
Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller |
Abstract
Read more
Phys. Rev. E, 83(5): 051921, 2011. See also arXiv:1011.1221.
 | Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann |
Abstract
Read more
Phys. Rev. Lett., 105(6): 068101, 2010. See also arXiv:1007.1871.
 | Cell Model Approach to Membrane Mediated Protein Interactions
Martin Michael Müller, Markus Deserno |
Membrane-deforming proteins can interact through the curvature
fields they create. In the case of many such proteins a cell model
approach can be used to calculate the energy per protein and
predict, whether it would lead to phase segregation or
bud-formation. Using covariant differential geometry exact results
are derived for the lateral pressure in terms of geometric
properties at the cell boundary. Numerical solutions of the exact
shape equations in the highly nonlinear regime are found and it is
seen that both phase segregation and bud formation can occur.
 Reduce
Read more Reduce
Read more
Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.
 | Hamiltonian formulation of surfaces with constant Gaussian curvature
Miguel Trejo, Martine Ben Amar, Martin Michael Müller |
Abstract
Read more
J. Phys. A: Math. Theor., 42(42): 425204, 2009.
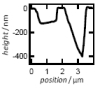 | Local Membrane Mechanics of Pore-Spanning Bilayers
Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.
 | Elasticity Mapping of Pore-Suspending Native Cell Membranes
Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
Small, 5(7): pp. 832-838, 2009.
 | Conical Defects in Growing Sheets
Martin Michael Müller, Martine Ben Amar, Jemal Guven |
Abstract
Read more
Phys. Rev. Lett., 101(15): 156104, 2008. See also arXiv:0807.1814.
 | How paper folds: bending with local constraints
Jemal Guven, Martin Michael Müller |
Abstract
Read more
J. Phys. A: Math. Theor., 41(5): 055203, 2008. See also arXiv:0712.0978.
 | Contact lines for fluid surface adhesion
Markus Deserno, Martin Michael Müller, Jemal Guven |
Abstract
Read more
Phys. Rev. E, 76(1): 011605, 2007. See also cond-mat/0703019.
 | Balancing torques in membrane-mediated interactions: Exact results and
numerical illustrations
Martin Michael Müller, Markus Deserno, Jemal Guven |
Torques on interfaces can be described by a divergence-free tensor
which is fully encoded in the geometry. This tensor consists of two
terms, one originating in the couple of the stress, the other capturing
an intrinsic contribution due to curvature. In analogy to the description
of forces in terms of a stress tensor, the torque on a particle can be
expressed as a line integral along any contour surrounding the particle.
Interactions between particles mediated by a fluid membrane are studied
within this framework. In particular, torque balance places a strong
constraint on the shape of the membrane. Symmetric two-particle
configurations admit simple analytical expressions which are valid
in the fully nonlinear regime; in particular, the problem may be
solved exactly in the case of two membrane-bound parallel cylinders.
This apparently simple system provides some flavor of the remarkably
subtle nonlinear behavior associated with membrane-mediated interactions.
 Reduce
Read more Reduce
Read more
Phys. Rev. E, 76(1): 011921, 2007. See also cond-mat/0702340.
 | Aggregation and vesiculation of membrane proteins by curvature-mediated
interactions
Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno |
Abstract
Read more
Nature 447(7143): pp. 461-464, 2007.
 | How to determine local elastic properties of lipid bilayer membranes
from atomic-force-microscope measurements: A theoretical analysis
Davood Norouzi, Martin Michael Müller, Markus Deserno |
Abstract
Read more
Phys. Rev. E, 74(6): 061914, 2006. See also cond-mat/0602662.
 | Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy
Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff |
We measure the elastic response of a free-standing lipid membrane to a local indentation by using an atomic force microscope. Starting point is a planar
gold-coated alumina substrate with a chemisorbed 3-mercaptopropionic acid
monolayer displaying circular pores of very well defined and tunable size, over
which bilayers composed of N,N,- dimethyl- N,N,- dioctadecylammonium bromide or
1,2 - dioleoyl - 3 - trimethylammonium - propane chloride were spread.
Centrally indenting these 'nanodrums' with an atomic force microscope tip yields
force-indentation curves, which we quantitatively analyze by solving the
corresponding shape equations of continuum curvature elasticity. Since the
measured response depends in a known way on the system geometry (pore size, tip
radius) and on material parameters (bending modulus, lateral tension), this opens
the possibility to monitor local elastic properties of lipid membranes in a
well-controlled setting.
 Reduce
Read more Reduce
Read more
Biophys. J., 91(1): pp. 217-226, 2006.
 | Interface mediated interactions between particles -- a geometrical approach
Martin Michael Müller, Markus Deserno, Jemal Guven |
Particles bound to an interface interact because they deform its shape.
The stresses that result are fully encoded in the geometry and described
by a divergence-free surface stress tensor. This stress tensor can be
used to express the force on a particle as a line integral along any
conveniently chosen closed contour that surrounds the particle. The
resulting expression is exact (i.e., free of any 'smallness' assumptions)
and independent of the chosen surface parametrization. Additional surface
degrees of freedom, such as vector fields describing lipid tilt, are readily
included in this formalism. As an illustration, we derive the exact force
for several important surface Hamiltonians in various symmetric two-particle
configurations in terms of the midplane geometry; its sign is evident in
certain interesting limits. Specializing to the linear regime, where the
shape can be analytically determined, these general expressions yield
force-distance relations, several of which have originally been derived
by using an energy based approach.
 Reduce
Read more Reduce
Read more
Phys. Rev. E, 72(6): 061407, 2005. See also cond-mat/0506019.
 | Geometry of surface-mediated interactions
Martin Michael Müller, Markus Deserno, Jemal Guven |
Abstract
Read more
Europhys. Lett., 69(3): pp. 482-488, 2005. See also cond-mat/0409043.
2. Books and collective works
3. Theses
-
Theoretical examinations of interface mediated interactions between colloidal particles,
diploma thesis (2004).
-
Theoretical studies of fluid membrane mechanics, dissertation (2007).
-
Symmetry breaking in bioelasticity, habilitation thesis (2015).
|


