Publications
-
Articles in scientific journals
-
Books
-
Theses
See also profiles on Publons,
Orcid or
Google Scholar.
1. Articles in scientific journals
 | Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic
Description of the Coiled-Coil Helix Bundle
Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller |
Abstract
Int. J. Mol. Sci., 25: 2481, 2024.
 | Flexoelectric fluid membrane vesicles in spherical confinement
Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller |
The morphology of spherically confined flexoelectric fluid membrane vesicles in an ex-
ternal uniform electric field is studied numerically. Due to the deformations induced by
the confinement, the membrane becomes polarized resulting in an interaction with the
external field. The equilibrium shapes of the vesicle without electric field can be clas-
sified in a geometrical phase diagram as a function of scaled area and reduced volume
[1, 2]. When the area of the membrane is only slightly larger than the area of the con-
fining sphere, a single axisymmetric invagination appears. A non-vanishing electric field
induces an additional elongation of the confined vesicle which is either perpendicular or
parallel depending on the sign of the electric field parameter. Higher values of the surface
area or the electric field parameter can reduce the symmetry of the system leading to
more complex folding. We present the resulting shapes and show that transition lines
are shifted in the presence of an electric field. The obtained folding patterns could be of
interest for biophysical and technological applications alike.
 Reduce
Read more Reduce
Read more
EPL, 131(1): 18001, 2020. See also arXiv:2006.04475.
 | Isometric bending requires local constraints on free edges
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
While the shape equations describing the equilibrium of an unstretchable thin sheet that is free
to bend are known, the boundary conditions that supplement these equations on free edges have remained elusive.
Intuitively, unstretchability is captured by a constraint on the metric within the bulk. Naïvely one would then
guess that this constraint is enough to ensure that the deformations determining the boundary conditions on these
edges respect the isometry constraint. If matters were this simple, unfortunately, it would imply unbalanced torques
(as well as forces) along the edge unless manifestly unphysical constraints are met by the boundary geometry. In this
article, we identify the source of the problem: not only the local arc-length but also the geodesic curvature need to
be constrained explicitly on all free edges. We derive the boundary conditions which follow. In contrast to conventional
wisdom, there is no need to introduce boundary layers. This framework is applied to isolated conical defects, both
with deficit as well, but more briefly, as surplus angles. Using these boundary conditions, we show that the lateral
tension within a circular cone of fixed radius is equal but opposite to the radial compression, and independent of
the deficit angle itself. We proceed to examine the effect of an oblique outer edge on this cone perturbatively
demonstrating that both the correction to the geometry as well as the stress distribution in the cone kicks in at
second order in the eccentricity of the edge.
 Reduce
Read more Reduce
Read more
Math. Mech. Solids, 24: 4051, 2019. See also arXiv:1904.05855.
 | Helical Superstructure of Intermediate Filaments
Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić |
Abstract
Read more
Phys. Rev. Lett., 122: 098101, 2019. See also arXiv:1803.04691.
 | Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows
Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller |
Abstract
Phys. Rev. E, 98: 043111, 2018. See also arXiv:1810.04500.
 | Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
Abstract
Read more
IOP Conf. Series: MSE, 186: 012021, 2017.
 | Squeezed helical elastica
Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach |
Abstract
Read more
Eur. Phys. J. E, 39: 114, 2016. See also arXiv:1606.03611.
 | How bio-filaments twist membranes
Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller |
Abstract
Soft Matter, 12: 5747, 2016.
 | Toroidal membrane vesicles in spherical confinement
Lila Bouzar, Ferhat Menas, Martin Michael Müller |
We investigate the morphology of a toroidal fluid membrane vesicle confined inside a spherical container.
The equilibrium shapes are assembled in a geometrical phase diagram as a function of scaled area and
reduced volume of the membrane. For small area the vesicle can adopt its free form. When increasing
the area, the membrane cannot avoid contact and touches the confining sphere along a circular contact line,
which extends to a zone of contact for higher area. The elastic energies of the equilibrium shapes are
compared to those of their confined counterparts of spherical topology to predict under which conditions a
topology change is favored energetically.
 Reduce
Read more Reduce
Read more
Phys. Rev. E, 92: 032721, 2015. See also arXiv:1509.00765.
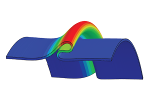 | Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate
Norbert Stoop, Martin Michael Müller |
Abstract
Read more
Int. J. Non-Linear Mech., 75: 115, 2015. See also arXiv:1503.05030.
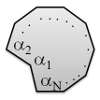 | Crunching Biofilament Rings
Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić |
We discuss a curious example for the collective mechanical behavior of coupled non-linear monomer units entrapped in a circular filament. Within a simple model we elucidate how multistability of monomer units and exponentially large degeneracy of the filament's ground state emerge as a collective feature of the closed filament. Surprisingly, increasing the monomer frustration, i.e., the bending prestrain within the circular filament, leads to a conformational softening of the system. The phenomenon, that we term polymorphic crunching, is discussed and applied to a possible scenario for membrane tube deformation by switchable dynamin or FtsZ filaments. We find an important role of cooperative inter-unit interaction for efficient ring induced membrane fission.
 Reduce
Read more Reduce
Read more
Europhys. Lett., 107(6): 68002, 2014. See also arXiv:1408.6787.
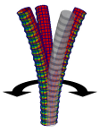 | Confotronic dynamics of tubular filaments
Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić |
Abstract
Read more
Soft Matter, 10(16): pp. 2836-2847, 2014. See also arXiv:1312.3106.
 | Whirling skirts and rotating cones
Jemal Guven, J. A. Hanna, Martin Michael Müller |
Abstract
New J. Phys., 15: 113055, 2013. See also arXiv:1306.2619.
 | Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo
Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte |
Abstract
J. Cell Sci., 126(8): 1806, 2013.
 | Dipoles in thin sheets
Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller |
Abstract
Read more
Eur. Phys. J. E, 36: 106, 2013. See also arXiv:1212.3262.
 | Fluid membrane vesicles in confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Abstract
Read more
New J. Phys., 14: 095021, 2012.
 | Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity
Martine Ben Amar, Martin Michael Müller, Miguel Trejo |
Abstract
Read more
New J. Phys., 14: 085014, 2012. Also featured in the Highlights of 2012.
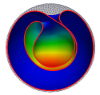 | Morphogenesis of membrane invaginations in spherical confinement
Osman Kahraman, Norbert Stoop, Martin Michael Müller |
Abstract
Read more
Europhys. Lett., 97(6): 68008, 2012. See also arXiv:1201.2518.
 | Conical instabilities on paper
Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo |
Abstract
Read more
J. Phys. A: Math. Theor., 45(1): 015203, 2012. See also arXiv:1107.5008.
 | Interface-mediated interactions: Entropic forces of curved membranes
Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller |
Abstract
Read more
Phys. Rev. E, 83(5): 051921, 2011. See also arXiv:1011.1221.
 | Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes
Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann |
We investigate the morphology of thin discs and rings growing in circumferential direction. Recent analytical results suggest that this growth produces symmetric excess cones (e-cones). We study the stability of such solutions considering self-contact and bending stress. We show that, contrary to what was assumed in previous analytical solutions, beyond a critical growth factor, no symmetric e-cone solution is energetically minimal any more. Instead, we obtain skewed e-cone solutions having lower energy, characterized by a skewness angle and repetitive spiral winding with increasing growth. These results are generalized to discs with varying thickness and rings with holes of different radii.
 Reduce
Read more Reduce
Read more
Phys. Rev. Lett., 105(6): 068101, 2010. See also arXiv:1007.1871.
 | Cell Model Approach to Membrane Mediated Protein Interactions
Martin Michael Müller, Markus Deserno |
Membrane-deforming proteins can interact through the curvature
fields they create. In the case of many such proteins a cell model
approach can be used to calculate the energy per protein and
predict, whether it would lead to phase segregation or
bud-formation. Using covariant differential geometry exact results
are derived for the lateral pressure in terms of geometric
properties at the cell boundary. Numerical solutions of the exact
shape equations in the highly nonlinear regime are found and it is
seen that both phase segregation and bud formation can occur.
 Reduce
Read more Reduce
Read more
Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.
 | Hamiltonian formulation of surfaces with constant Gaussian curvature
Miguel Trejo, Martine Ben Amar, Martin Michael Müller |
Abstract
Read more
J. Phys. A: Math. Theor., 42(42): 425204, 2009.
 | Local Membrane Mechanics of Pore-Spanning Bilayers
Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.
 | Elasticity Mapping of Pore-Suspending Native Cell Membranes
Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
Small, 5(7): pp. 832-838, 2009.
 | Conical Defects in Growing Sheets
Martin Michael Müller, Martine Ben Amar, Jemal Guven |
Abstract
Read more
Phys. Rev. Lett., 101(15): 156104, 2008. See also arXiv:0807.1814.
 | How paper folds: bending with local constraints
Jemal Guven, Martin Michael Müller |
Abstract
Read more
J. Phys. A: Math. Theor., 41(5): 055203, 2008. See also arXiv:0712.0978.
 | Contact lines for fluid surface adhesion
Markus Deserno, Martin Michael Müller, Jemal Guven |
When a fluid surface adheres to a substrate, the location of the
contact line adjusts in order to minimize the overall energy. This
adhesion balance implies boundary conditions which depend on the
characteristic surface deformation energies. We develop a general
geometrical framework within which these conditions can be
systematically derived.
We treat both adhesion to a rigid substrate as well as adhesion
between two fluid surfaces, and illustrate our general results for
several important Hamiltonians involving both curvature and
curvature gradients. Some of these have previously been studied
using very different techniques, others are to our knowledge new.
What becomes clear in our approach is that, except for capillary
phenomena, these boundary conditions are not the manifestation
of a local force balance, even if the concept of surface stress is
properly generalized. Hamiltonians containing higher order surface
derivatives are not just sensitive to boundary translations but also
notice changes in slope or even curvature.
Both the necessity and the functional form of the corresponding
additional contributions follow readily from our treatment.
 Reduce
Read more Reduce
Read more
Phys. Rev. E, 76(1): 011605, 2007. See also cond-mat/0703019.
Also featured in the Virtual Journal of Biological Physics Research.
 | Balancing torques in membrane-mediated interactions: Exact results and
numerical illustrations
Martin Michael Müller, Markus Deserno, Jemal Guven |
Abstract
Read more
Phys. Rev. E, 76(1): 011921, 2007. See also cond-mat/0702340.
Also featured in the Virtual Journal of Biological Physics Research.
 | Aggregation and vesiculation of membrane proteins by curvature-mediated
interactions
Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno |
Abstract
Read more
Nature 447(7143): pp. 461-464, 2007.
 | How to determine local elastic properties of lipid bilayer membranes
from atomic-force-microscope measurements: A theoretical analysis
Davood Norouzi, Martin Michael Müller, Markus Deserno |
Abstract
Read more
Phys. Rev. E, 74(6): 061914, 2006. See also cond-mat/0602662.
Also featured in the Virtual Journal of Biological Physics Research.
 | Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy
Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff |
Abstract
Read more
Biophys. J., 91(1): pp. 217-226, 2006.
 | Interface mediated interactions between particles -- a geometrical approach
Martin Michael Müller, Markus Deserno, Jemal Guven |
Abstract
Read more
Phys. Rev. E, 72(6): 061407, 2005. See also cond-mat/0506019.
Also featured in the Virtual Journal of Biological Physics Research.
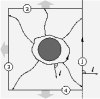 | Geometry of surface-mediated interactions
Martin Michael Müller, Markus Deserno, Jemal Guven |
Abstract
Read more
Europhys. Lett., 69(3): pp. 482-488, 2005. See also cond-mat/0409043.
2. Books
-
New Trends in the Physics and Mechanics of Biological Systems
Lecture Notes of the Les Houches Summer School, vol. 92 (Oxford University Press, 2011),
edited by Martine Ben Amar, Alain Goriely, Martin Michael Müller and Leticia Cugliandolo.
Chapter 9:
The physics of the cell membrane
Martin Michael Müller and Martine Ben Amar.
3. Theses
-
Theoretical examinations of interface mediated interactions between colloidal particles,
diploma thesis (2004).
-
Theoretical studies of fluid membrane mechanics, dissertation (2007).
-
Symmetry breaking in bioelasticity, habilitation thesis (2015).
|


