Homepage of Martin Michael Müller

Publications

Articles in scientific journals
Books
Theses

See also profiles on Publons, Orcid or Google Scholar.

1. Articles in scientific journals

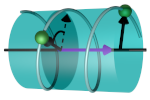Conformational Space of the Translocation Domain of Botulinum Toxin: Atomistic Modeling and Mesoscopic Description of the Coiled-Coil Helix Bundle

Alexandre Delort, Grazia Cottone, Thérèse E. Malliavin, Martin Michael Müller

Abstract

Int. J. Mol. Sci., 25: 2481, 2024.

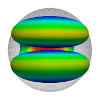Flexoelectric fluid membrane vesicles in spherical confinement

Niloufar Abtahi, Lila Bouzar, Nadia Saidi-Amroun, Martin Michael Müller
EPL, 131(1): 18001, 2020. See also arXiv:2006.04475.

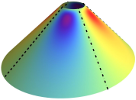Isometric bending requires local constraints on free edges

Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo
While the shape equations describing the equilibrium of an unstretchable thin sheet that is free to bend are known, the boundary conditions that supplement these equations on free edges have remained elusive. Intuitively, unstretchability is captured by a constraint on the metric within the bulk. Naïvely one would then guess that this constraint is enough to ensure that the deformations determining the boundary conditions on these edges respect the isometry constraint. If matters were this simple, unfortunately, it would imply unbalanced torques (as well as forces) along the edge unless manifestly unphysical constraints are met by the boundary geometry. In this article, we identify the source of the problem: not only the local arc-length but also the geodesic curvature need to be constrained explicitly on all free edges. We derive the boundary conditions which follow. In contrast to conventional wisdom, there is no need to introduce boundary layers. This framework is applied to isolated conical defects, both with deficit as well, but more briefly, as surplus angles. Using these boundary conditions, we show that the lateral tension within a circular cone of fixed radius is equal but opposite to the radial compression, and independent of the deficit angle itself. We proceed to examine the effect of an oblique outer edge on this cone perturbatively demonstrating that both the correction to the geometry as well as the stress distribution in the cone kicks in at second order in the eccentricity of the edge.

Reduce Read more
Math. Mech. Solids, 24: 4051, 2019. See also arXiv:1904.05855.

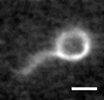Helical Superstructure of Intermediate Filaments

Lila Bouzar, Martin Michael Müller, René Messina, Bernd Nöding, Sarah Köster, Hervé Mohrbach, Igor M. Kulić

Abstract Read more

Phys. Rev. Lett., 122: 098101, 2019. See also arXiv:1803.04691.

Vesicle dynamics in confined steady and harmonically modulated Poiseuille flows

Zakaria Boujja, Chaouqi Misbah, Hamid Ez-Zahraouy, Abdelilah Benyoussef, Thomas John, Christian Wagner, Martin Michael Müller

Abstract

Phys. Rev. E, 98: 043111, 2018. See also arXiv:1810.04500.

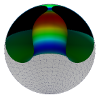Confining a fluid membrane vesicle of toroidal topology in an adhesive hard sphere

Lila Bouzar, Ferhat Menas, Martin Michael Müller

Abstract Read more

IOP Conf. Series: MSE, 186: 012021, 2017.

Squeezed helical elastica

Lila Bouzar, Martin Michael Müller, Pierre Gosselin, Igor M. Kulić, Hervé Mohrbach

Abstract Read more

Eur. Phys. J. E, 39: 114, 2016. See also arXiv:1606.03611.

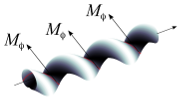How bio-filaments twist membranes

Julien Fierling, Albert Johner, Igor M. Kulić, Hervé Mohrbach, Martin Michael Müller

Abstract

Soft Matter, 12: 5747, 2016.

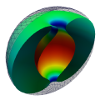Toroidal membrane vesicles in spherical confinement

Lila Bouzar, Ferhat Menas, Martin Michael Müller

Abstract Read more

Phys. Rev. E, 92: 032721, 2015. See also arXiv:1509.00765.

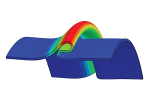Non-linear buckling and symmetry breaking of a soft elastic sheet sliding on a cylindrical substrate

Norbert Stoop, Martin Michael Müller

Abstract Read more

Int. J. Non-Linear Mech., 75: 115, 2015. See also arXiv:1503.05030.

Crunching Biofilament Rings

Julien Fierling, Martin Michael Müller, Hervé Mohrbach, Albert Johner, Igor M. Kulić

Abstract Read more

Europhys. Lett., 107(6): 68002, 2014. See also arXiv:1408.6787.

Confotronic dynamics of tubular filaments

Osman Kahraman, Hervé Mohrbach, Martin Michael Müller, Igor M. Kulić

Abstract Read more

Soft Matter, 10(16): pp. 2836-2847, 2014. See also arXiv:1312.3106.

Whirling skirts and rotating cones

Jemal Guven, J. A. Hanna, Martin Michael Müller
Steady, dihedrally symmetric patterns with sharp peaks may be observed on a spinning skirt, lagging behind the material flow of the fabric. These qualitative features are captured with a minimal model of traveling waves on an inextensible, flexible, generalized-conical sheet rotating about a fixed axis. Conservation laws are used to reduce the dynamics to a quadrature describing a particle in a three-parameter family of potentials. One parameter is associated with the stress in the sheet, aNoether is the current associated with rotational invariance, and the third is a Rossby number which indicates the relative strength of Coriolis forces. Solutions are quantized by enforcing a topology appropriate to a skirt and a particular choice of dihedral symmetry. A perturbative analysis of nearly axisymmetric cones shows that Coriolis effects are essential in establishing skirt-like solutions. Fully non-linear solutions with three-fold symmetry are presented which bear a suggestive resemblance to the observed patterns.

Reduce
New J. Phys., 15: 113055, 2013. See also arXiv:1306.2619.

Myotubularin and PtdIns3P remodel the sarcoplasmic reticulum in muscle in vivo

Leonela Amoasii, Karim Hnia, Gaëtan Chicanne, Andreas Brech, Belinda Simone Cowling, Martin Michael Müller, Yannick Schwab, Pascale Koebel, Arnaud Ferry, Bernard Payrastre, Jocelyn Laporte

Abstract

J. Cell Sci., 126(8): 1806, 2013.

Dipoles in thin sheets

Jemal Guven, J. A. Hanna, Osman Kahraman, Martin Michael Müller

Abstract Read more

Eur. Phys. J. E, 36: 106, 2013. See also arXiv:1212.3262.

Fluid membrane vesicles in confinement

Osman Kahraman, Norbert Stoop, Martin Michael Müller
We numerically study the morphology of fluid membrane vesicles with prescribed volume and surface area in confinement. For spherical confinement we observe axisymmetric invaginations that transform into ellipsoidal invaginations a the area of the vesicle is increased, followed by a transition into stomatocyte-like shapes. We provide a detailed analysis of the axisymmetric shapes and investigate the effect of the spontaneous curvature of the membrane as a possible mechanism for shape regulation. We show that the observed morphologies are stable under small geometric deformations of the confinement. The results could help to understand the role of mechanics in the complex folding patterns of biological membranes.

Reduce Read more
New J. Phys., 14: 095021, 2012.

Petal shapes of sympetaleous flowers: the interplay between growth, geometry and elasticity

Martine Ben Amar, Martin Michael Müller, Miguel Trejo
The growth of a thin elastic sheet imposes constraints on its geometry such as its Gaussian curvature K_G. In this paper, we construct the shapes of sympetalous bell-shaped flowers with a constant Gaussian curvature. Minimizing the bending energies of both the petal and the veins, we are able to predict quantitatively the global shape of these flowers. We discuss two toy problems where the Gaussian curvature is either negative or positive. In the former case the axisymmetric pseudosphere turns out to mimic the correct shape before edge curling; in the latter case, singularities of the mathematical surface coincide with strong veins. Using a variational minimization of the elastic energy, we find that the optimal number for the veins is either four, five or six, a number which is deceptively close to the statistics on real flowers in nature.

Reduce Read more
New J. Phys., 14: 085014, 2012. Also featured in the Highlights of 2012.

Morphogenesis of membrane invaginations in spherical confinement

Osman Kahraman, Norbert Stoop, Martin Michael Müller

Abstract Read more

Europhys. Lett., 97(6): 68008, 2012. See also arXiv:1201.2518.

Conical instabilities on paper

Jemal Guven, Martin Michael Müller, Pablo Vázquez-Montejo

Abstract Read more

J. Phys. A: Math. Theor., 45(1): 015203, 2012. See also arXiv:1107.5008.

Interface-mediated interactions: Entropic forces of curved membranes

Pierre Gosselin, Hervé Mohrbach, Martin Michael Müller

Abstract Read more

Phys. Rev. E, 83(5): 051921, 2011. See also arXiv:1011.1221.

Self-Contact and Instabilities in the Anisotropic Growth of Elastic Membranes

Norbert Stoop, Falk K. Wittel, Martine Ben Amar, Martin Michael Müller, Hans J. Herrmann
We investigate the morphology of thin discs and rings growing in circumferential direction. Recent analytical results suggest that this growth produces symmetric excess cones (e-cones). We study the stability of such solutions considering self-contact and bending stress. We show that, contrary to what was assumed in previous analytical solutions, beyond a critical growth factor, no symmetric e-cone solution is energetically minimal any more. Instead, we obtain skewed e-cone solutions having lower energy, characterized by a skewness angle and repetitive spiral winding with increasing growth. These results are generalized to discs with varying thickness and rings with holes of different radii.

Reduce Read more
Phys. Rev. Lett., 105(6): 068101, 2010. See also arXiv:1007.1871.

Cell Model Approach to Membrane Mediated Protein Interactions

Martin Michael Müller, Markus Deserno

Abstract Read more

Prog. Theor. Phys. Suppl., 184: pp. 351-363, 2010.

Hamiltonian formulation of surfaces with constant Gaussian curvature

Miguel Trejo, Martine Ben Amar, Martin Michael Müller
Dirac's method for constrained Hamiltonian systems is used to describe surfaces of constant Gaussian curvature. A geometrical free energy, for which these surfaces are equilibrium states, is introduced and interpreted as an action. An equilibrium surface can then be generated by the evolution of a closed space curve. Since the underlying action depends on second derivatives, the velocity of the curve and its conjugate momentum must be included in the set of phase space variables. Furthermore, the action is linear in the acceleration of the curve and possesses a local symmetry---reparametrization invariance---which implies primary constraints in the canonical formalism. These constraints are incorporated into the Hamiltonian through Lagrange multiplier functions, that are identified as the components of the acceleration of the curve. The formulation leads to four first order partial differential equations, one for each canonical variable. With the appropriate choice of parametrization only one of these equations has to be solved to obtain the surface which is swept out by the evolving space curve. To illustrate the formalism, several evolutions of pseudospherical surfaces are discussed.

Reduce Read more
J. Phys. A: Math. Theor., 42(42): 425204, 2009.

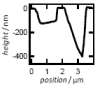Local Membrane Mechanics of Pore-Spanning Bilayers

Ingo Mey, Milena Stephan, Eva K. Schmitt, Martin Michael Müller, Martine Ben Amar, Claudia Steinem, Andreas Janshoff

Abstract Read more

J. Am. Chem. Soc., 131(20): pp. 7031-7039, 2009.

Elasticity Mapping of Pore-Suspending Native Cell Membranes

Bärbel Lorenz, Ingo Mey, Siegfried Steltenkamp, Tamir Fine, Christina Rommel, Martin Michael Müller, Alexander Maiwald, Joachim Wegener, Claudia Steinem, Andreas Janshoff

Abstract Read more

Small, 5(7): pp. 832-838, 2009.

Conical Defects in Growing Sheets

Martin Michael Müller, Martine Ben Amar, Jemal Guven

Abstract Read more

Phys. Rev. Lett., 101(15): 156104, 2008. See also arXiv:0807.1814.

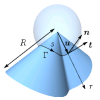How paper folds: bending with local constraints

Jemal Guven, Martin Michael Müller
A variational framework is introduced to describe how a surface bends when it is subject to local constraints on its geometry. This framework is applied to describe the patterns of a folded sheet of paper. The unstretchability of paper implies a constraint on the surface metric; bending is penalized by an energy quadratic in mean curvature. The local Lagrange multipliers enforcing the constraint are identified with a conserved tangential stress that couples to the extrinsic curvature of the sheet. The framework is illustrated by examining the deformation of a flat sheet into a generalized cone.

Reduce Read more
J. Phys. A: Math. Theor., 41(5): 055203, 2008. See also arXiv:0712.0978.

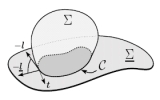Contact lines for fluid surface adhesion

Markus Deserno, Martin Michael Müller, Jemal Guven
When a fluid surface adheres to a substrate, the location of the contact line adjusts in order to minimize the overall energy. This adhesion balance implies boundary conditions which depend on the characteristic surface deformation energies. We develop a general geometrical framework within which these conditions can be systematically derived. We treat both adhesion to a rigid substrate as well as adhesion between two fluid surfaces, and illustrate our general results for several important Hamiltonians involving both curvature and curvature gradients. Some of these have previously been studied using very different techniques, others are to our knowledge new. What becomes clear in our approach is that, except for capillary phenomena, these boundary conditions are not the manifestation of a local force balance, even if the concept of surface stress is properly generalized. Hamiltonians containing higher order surface derivatives are not just sensitive to boundary translations but also notice changes in slope or even curvature. Both the necessity and the functional form of the corresponding additional contributions follow readily from our treatment.

Reduce Read more
Phys. Rev. E, 76(1): 011605, 2007. See also cond-mat/0703019.
Also featured in the Virtual Journal of Biological Physics Research.

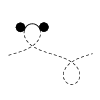Balancing torques in membrane-mediated interactions: Exact results and numerical illustrations

Martin Michael Müller, Markus Deserno, Jemal Guven
Torques on interfaces can be described by a divergence-free tensor which is fully encoded in the geometry. This tensor consists of two terms, one originating in the couple of the stress, the other capturing an intrinsic contribution due to curvature. In analogy to the description of forces in terms of a stress tensor, the torque on a particle can be expressed as a line integral along any contour surrounding the particle. Interactions between particles mediated by a fluid membrane are studied within this framework. In particular, torque balance places a strong constraint on the shape of the membrane. Symmetric two-particle configurations admit simple analytical expressions which are valid in the fully nonlinear regime; in particular, the problem may be solved exactly in the case of two membrane-bound parallel cylinders. This apparently simple system provides some flavor of the remarkably subtle nonlinear behavior associated with membrane-mediated interactions.

Reduce Read more
Phys. Rev. E, 76(1): 011921, 2007. See also cond-mat/0702340.
Also featured in the Virtual Journal of Biological Physics Research.

Aggregation and vesiculation of membrane proteins by curvature-mediated interactions

Benedict J. Reynwar, Gregoria Illya, Vagelis A. Harmandaris, Martin Michael Müller, Kurt Kremer, Markus Deserno

Abstract Read more

Nature 447(7143): pp. 461-464, 2007.

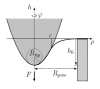How to determine local elastic properties of lipid bilayer membranes from atomic-force-microscope measurements: A theoretical analysis

Davood Norouzi, Martin Michael Müller, Markus Deserno

Abstract Read more

Phys. Rev. E, 74(6): 061914, 2006. See also cond-mat/0602662.
Also featured in the Virtual Journal of Biological Physics Research.

Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy

Siegfried Steltenkamp, Martin Michael Müller, Markus Deserno, Christian Hennesthal, Claudia Steinem, Andreas Janshoff

Interface mediated interactions between particles -- a geometrical approach

Martin Michael Müller, Markus Deserno, Jemal Guven
Particles bound to an interface interact because they deform its shape. The stresses that result are fully encoded in the geometry and described by a divergence-free surface stress tensor. This stress tensor can be used to express the force on a particle as a line integral along any conveniently chosen closed contour that surrounds the particle. The resulting expression is exact (i.e., free of any 'smallness' assumptions) and independent of the chosen surface parametrization. Additional surface degrees of freedom, such as vector fields describing lipid tilt, are readily included in this formalism. As an illustration, we derive the exact force for several important surface Hamiltonians in various symmetric two-particle configurations in terms of the midplane geometry; its sign is evident in certain interesting limits. Specializing to the linear regime, where the shape can be analytically determined, these general expressions yield force-distance relations, several of which have originally been derived by using an energy based approach.

Reduce Read more
Phys. Rev. E, 72(6): 061407, 2005. See also cond-mat/0506019.
Also featured in the Virtual Journal of Biological Physics Research.

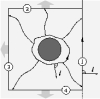Geometry of surface-mediated interactions

Martin Michael Müller, Markus Deserno, Jemal Guven

Abstract Read more

Europhys. Lett., 69(3): pp. 482-488, 2005. See also cond-mat/0409043.

2. Books

New Trends in the Physics and Mechanics of Biological Systems
Lecture Notes of the Les Houches Summer School, vol. 92 (Oxford University Press, 2011),
edited by Martine Ben Amar, Alain Goriely, Martin Michael Müller and Leticia Cugliandolo.

Chapter 9:
The physics of the cell membrane
Martin Michael Müller and Martine Ben Amar.

3. Theses

Theoretical examinations of interface mediated interactions between colloidal particles, diploma thesis (2004).

Theoretical studies of fluid membrane mechanics, dissertation (2007).

Symmetry breaking in bioelasticity, habilitation thesis (2015).